Calculate more precisely
Before working with equal total payments loans, you should beforehand these four concepts:
- The amount of the amortization payments( as ), which are equal in all period, except on the last one. This variable shows us the amount that we have to pay in each period.
- The amount of the interest payments ( Is ), which depend on the outstanding balance or outstanding principal ( Cs ) and the rate of interest of each year ( is ). This variable shows us the part of the amortization payment ( as ) which is used to pay the accrued interest.
- The amount of principal or capital repayment ( As ), which is obtained on subtracting the interest payment ( Is ) from the amortization payment ( as ). This variable shows us the part of the amortization payment ( as ) which is used to repay the debt.
- The amount of the outstanding balance or outstanding principal ( Cs ), which depend on the principal repayment ( As ), because it is obtained on substracting the principal repayment of this period ( As ) from the outstanding balance of the previous period. This variable shows us the indebtedness at any time.
You have to know that the index rate ( irs ) of each year has to be adjusted by the margin or spread ( d ), with the exception of the first year interest rate, which is not subject to this type of adjustment. The adjustment is calculated on the basis of the following formula:
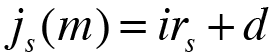
With the above formula you can obtain the nominal rate of interest of this period ( j(m) ) and you need the Effective rate of interest per time unit ( i(m) ), this is why you have to do the following conversion:

Once calculated the rate of interest applied to each period, you have to calculate the different variables explained above:
- First of all, you have to calculate the interest payment ( Is ) from the outstanding balance or outstanding principal of the previous period ( Cs-1 ) and the effective rate of interest per time unit ( is(m) ) of this period, using the following formula:

- Once the interest payment ( Is ) is calculated, you have to calculate the principal or capital repayment ( As ) as difference between the amortization payment ( as ) and the interest payment ( Is ):
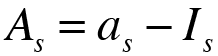
- Lastly, you have to calculate the outstanding balance or outstanding principal ( Cs ) as difference between the outstanding balance or outstanding principal of the previous period ( Cs-1 ) and the principal or capital repayment of this period ( As ):

The last amortization payment ( an ) has to be calculated, because is different from the rest of the amortization payments, this is because the last one is a adjustment payment. You can calculate this one from the outstanding balance or outstanding principal of the previous period ( Cs-1 ) by multiplying it by the effective rate of interest per time unit ( is(m) ):
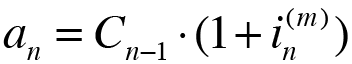
But, how do you know what is the last amortization payment?
- Because you have reached the maximum years, so you have to pay the same of the rest periods, plus the outstanding debt. Or as explained before, you have to calculate it from the outstanding balance or outstanding principal of the previous period ( Cs-1 ).
- Because you have paid back the debt before the maximum years. It is recognizable when the outstanding balance or outstanding principal ( Cs ) is negative, then you have to calculate it from the outstanding balance or outstanding principal of the previous period ( Cs-1 ).
|