Cuando realizamos préstamos con términos amortizativos constantes nos interesa conocer cuatro variables diferentes:

• La cuantía de los términos amortizativos ( a_s ), que en este tipo de operaciones será siempre de igual cuantía, excepto en el último término. Esta variable nos muestra la cuantía a pagar en cada uno de los períodos.
• La cuantía de las cuotas de interés ( I_s ), que dependerán del capital vivo o pendiente de amortizar ( C_s ) y el tipo de interés de cada período ( i_s ). Esta variable nos muestra la parte de los términos amortizativos ( a_s ) que va destinada al pago de intereses.
• La cuantía de las cuotas de amortización ( A_s ), que se obtendrá a partir de restarle a los términos amortizativos ( a_s ) las cuotas de interés ( I_s ). Esta variable nos muestra la parte de los términos amortizativos ( a_s ) que va destinada a la devolución de capital o deuda.
• La cuantía del capital vivo o pendiente de amortizar ( C_s ), que dependerá de las cuotas de amortización ( A_s ), ya que se obtiene a partir de la deuda pendiente de devolver en el periodo anterior ( C_s-1 ) menos la cuota de amortización de ese periodo ( A_s ). Esta variable nos muestra la deuda pendiente de devolver en cada periodo tras haber realizado el pago de los términos amortizativos.

Hay que tener en cuenta que los índices de referencia ( ir_s ) de cada año están sujetos a una corrección mediante la aplicación de un diferencial ( d ), con la excepción del primer año, que no está sujeto a este tipo de corrección. La corrección se realizará mediante la siguiente fórmula:

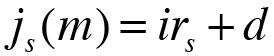
Al tratarse de un préstamo, el diferencial se suma siempre por defecto, ya que no tendría gran sentido restárselo (suele restarse en las operaciones de ahorro). Aún así, si desea poner un diferencial negativo solo tiene que poner el símbolo - antes del diferencial y se obtendrán los términos amortizativos de cada período ( a_s ) con el diferencial negativo.

Pero con la anterior fórmula obtenemos el tipo de interés nominal de ese año ( j(m) ) y nosotros tenemos que trabajar con el tipo de interés efectivo subperiodal ( i^(m) ), por lo que es necesario realizar la siguiente conversión:

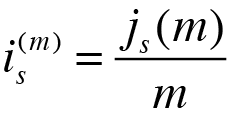
Una vez calculados los tipos de interés aplicados a cada período, procedemos al cálculo de las distintas variables anteriormente explicadas:

• En primer lugar calculamos la cuantía de la cuota de interés ( I_s ) a partir de el capital vivo del periodo anterior ( C_s-1 ) y el tipo de interés efectivo subperiodal ( i_s^(m) ) de ese período, con la siguiente fórmula:

• Una vez calculada la cuota de interés ( I_s ), procedemos al cálculo de la cuota de amortización ( A_s ) como diferencia entre el término amortizativo ( a_s ) y la cuota de interés ( I_s ):

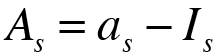
• Por último obtenemos el capital vivo o pendiente de amortizar ( C_s ), a partir del capital vivo del periodo anterior ( C_s-1 ), restándole la cuota de amortización de ese periodo( A_s ):

El último término amortizativo ( a_n ) habrá que calcularlo, ya que (como hemos dicho anteriormente) es distinto al resto, debido a que se trata de un término amortizativo de ajuste. Este se obtendrá a partir del capital vivo del periodo anterior ( C_n-1 ) multiplicándolo por el tipo de interés efectivo subperiodal ( i_n^(m) ):

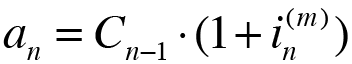
Pero, ¿cómo sabemos cuál es el último término amortizativo?

• Porque hayas llegado al máximo de años señalado, por lo que en el último periodo se pagará lo mismo que en el resto, más la deuda pendiente de amortizar en ese periodo. O como hemos explicado anteriormente, se va al periodo anterior y se calcula a partir del capital vivo.
• Porque hayas devuelto la deuda antes de alcanzar el máximo de años. Esto se aprecia cuando al calcular el capital vivo ( C_s ) sale negativo, entonces se irá al perido anterior y se realizará el cálculo anteriormente explicado.